ECC工作原理
ECC检验与纠错_Christal_RJ的博客-CSDN博客
ECC有三种常用的算法，包括汉明码(hamming code)、RS码(Reed Solomon code)和BCH码。其中汉明码是FSMC模块的硬件ECC所采用的校验方式。
ECC常见算法
汉明码
以1 Byte的数据包为例
为计算ECC值，数据包中的比特数据要先进行分割，如1/2组(Halfs)、1/4组(Fourths)、1/8(Bits)组等，直到其精度达到单个比特为止，以8 bit即1 Byte的数据包为例进行说明，
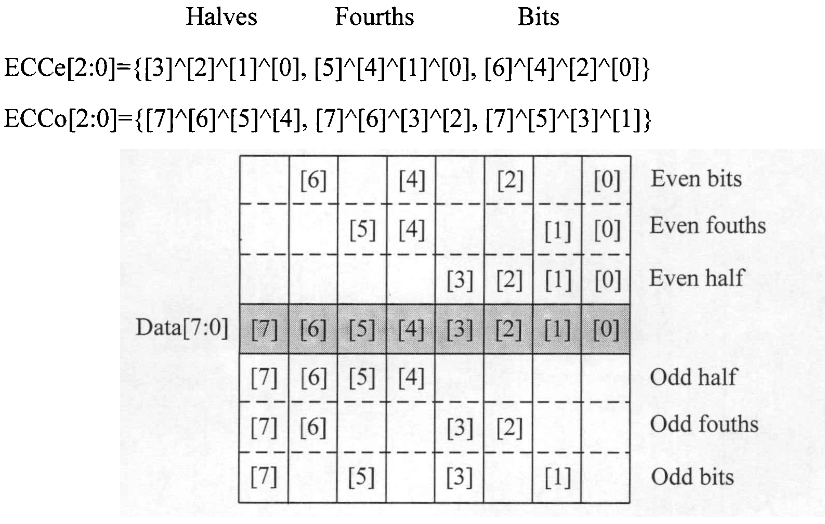每$2^n-1$比特数据计算得到n比特ECC值，而该汉明算法需要一对ECC值(偶校验值ECCe和奇校验值ECCo，如上图所示，^表示异或)，因此共需要2n比特。
计算之后，原数据包和ECC数值被写入。稍后，原数据包读取出，此时ECC值将重新计算。如果新计算的ECC不同于先前编入的ECC，那么表明数据在读写过程中出错。
```ad-example
title: 示例
type=例：原始数据为01010101，计算并存入的ECC值是ECCe=000、ECCo=000。若其中有1个单一的比特出现错误，出错后的数据是01010001。计算新ECC值如下：
```
检验是否发生错误
通过计算Error进行判断：
Error[2:0]=ECCe ⊕ ECCo ⊕ ECCe’ ⊕ ECCo’
Error=111表示发生一位错误，Error=000表示没有发生错误，而 Error不是上述两个值时，表示发生2位及以上错误，出现的可能性非常低。
检测错误发生位置
通过计算Error_Loc进行判断：
Error_Loc[2:0]=ECCo⊕ECCo’ = 000⊕010 = 010
Error_Loc=010，表示Data的第二位（data[3]）发生错误，对应取反即可。
按照此思路，8比特Data汉明校验元生成电路如下图所示：
8比特Data汉明校验元生成电路由14个异或门组成
以4 Byte的数据包为例
将汉明校验的计算推广到4个字节作为一个分组块，现在字节和比特排列如下图所示：
现在计算偶校验值ECCe和奇校验值ECCo如下：
行校验码：
行偶校验码：
Byte-Even half = B1⊕B0
Byte-Even bits = B2⊕B0
行奇校验码：
Byte-Odd half = B3⊕B2
Byte-Odd bits = B3⊕B1
其中，Bi = Di[7]⊕Di[6]⊕Di[5]⊕Di[4]⊕Di[3]⊕Di[2]⊕Di[1]⊕Di[0]
列校验码：
列偶校验码：
Bit-Even half = D[3]⊕D[2]⊕D[1]⊕D[0]
Bit-Even fourth = D[5]⊕D[4]⊕D[1]⊕D[0]
Bit-Even bits = D[6]⊕D[4]⊕D[2]⊕D[0]
列奇校验码：
Bit-Odd half = D[7]⊕D[6]⊕D[5]⊕D[4]
Bit-Odd fourth = D[7]⊕D[6]⊕D[3]⊕D[2]
Bit-Odd bits = D[7]⊕D[5]⊕D[3]⊕D[1]
其中，D[i]=D3[i]⊕D2[i]⊕D1[i]⊕DO[i]（每个字节对应位置都加入计算）
![]() 例： 假设4个字节数据Byte3~Byte1分别是01010101,11001100,10001000,00100010，计算得到的ECCe=00000, ECCo=00000，若此时 Byte1发生错误变成10000000(第3位从1翻转成0)，计算得到新的ECCe=10100，ECCo'=01011，因此通过计算Error=11111，表示发生一位错误，计算Error_Loc=01011,表示该位错误发生在01字节即 Byte1的第011位即第3位
BCH码
BCH码是循环码中的一个重要子类，它具有纠正多个错误的能力,广泛应用于移动通信和卫星通信中。BCH码有着严密的代数结构，是目前研究得比较透彻的一种码。关于BCH码编码的原理详解可参考：【举例子详细分析】BCH码(BCH code)
RS码
里德-所罗门(Reed-Solomon，RS）码是BCH码的一个重要分类，RS码是一种非二进制的BCH码，具有较强的纠错能力。
LDPC码
LDPC码即低密度奇偶校验码（Low Density Parity Check Code，LDPC），它由Robert G.Gallager博士于1963年提出的一类具有稀疏校验矩阵的线性分组码，不仅有逼近Shannon限的良好性能，而且译码复杂度较低，结构灵活，是近年信道编码领域的研究热点。
LDPC码是一种分组码，其校验矩阵只含有很少量非零元素（稀疏矩阵）。
reference
[1]陈武. Nand Flash纠错码的设计研究[D].浙江大学,2011.
